龙珠超,全王所面临的5大危机,全宇宙最高神并不是高枕无忧
失踪的正方形去哪儿了?数学中有趣的几何视觉错觉
失踪的正方形是什么?
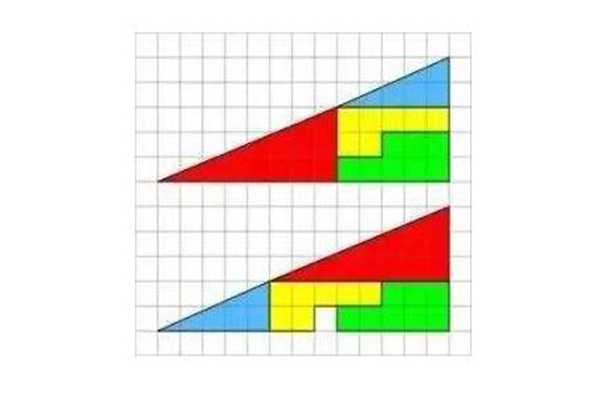
失踪的正方形实际上就是数学中的一种几何视觉错觉,这是在1953年由一个纽约的业余魔术师保罗·嘉理发明的,不过这样的裁剪原理在1860年就被数学界所知,失踪的正方形其实就是2种几何拼接方法,拼完的每一个图形都是13乘5的三角形,但是只有其中的一种方法少了一个1乘1的正方形。

在拼接的过程中并没有对图形动手脚,只是将原本的三角形分成了四个特定的图形,然后再重新拼接,可是新的三角形却少了一块,这让很多人疑惑不解,到底是哪儿丢失了这一个正方形的面积呢?
失踪的正方形去哪儿了?
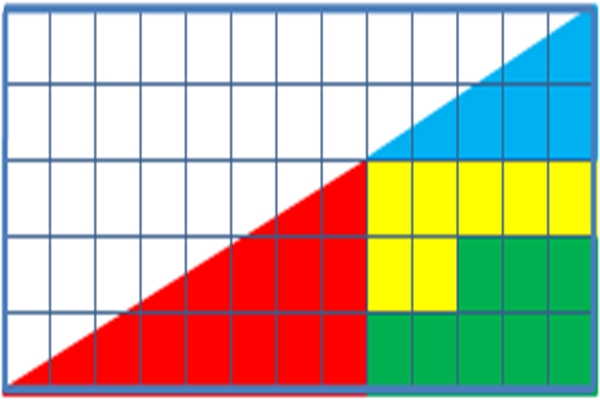
其实第二种拼法拼成的三角形,并不是真正的三角形,红色部分和蓝色部分的倾斜度有轻微的差异,所以这时候的“三角形”就会多出一条十分细小的平行四边形的边,这就是那块失踪的正方形多出来的面积,如果将两张图重合,就会明显的发现,而这个细长的平行四边形就恰好占据了一格的面积。

所以对于没有精确运算,只是凭借肉眼观察的人眼来说,这样细微的差别根本无法看到,所以就会显得这个失踪的正方形很突兀,好像十分不合情理,这就像晃动的方块幻觉一样,所以我们就用算法来精确的证实一下吧!

根据图上的格子来看,四个图形占了32个单位,但是总三角形是13乘5的,所以通过计算得出了32.5个单位,这一下就多了0.5个单位,因为蓝色三角形的长宽比是5:2,而红色是8:3,明显不是一个长宽比,所以斜边实际上缩短了。
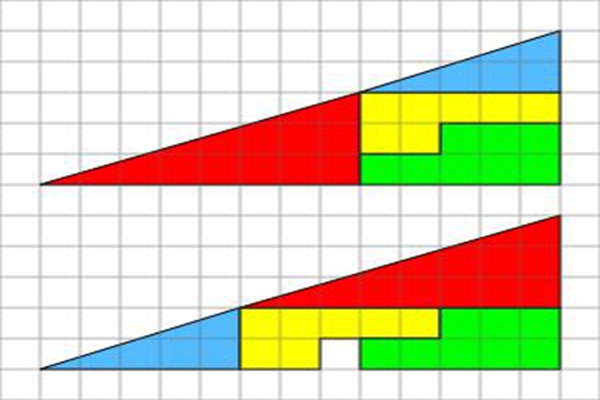
而总共缩短的长度是一个单位的1/28,这一点细微的溢出,在人眼看来并不明显,所以当这个溢出的平行四边形合拢时,就是刚好一格的大小,也就正好是失踪的正方形。
结语:在数学上还有很多有趣的现象,比如毕达哥拉斯树,就是利用勾股定理所画出的一棵树,所以说数学其实也可以很有意思。
显示全文
相关文章
-
-
海底有九万米吗,目前测得最深1万多米/再深有大恐怖
-
智能手机是谁发明的?这对于如今生活有哪些影响
-
硅基生命被发现了 已知的硅基生命有哪些
-
黑洞会吞噬整个宇宙,源于黑洞的特性?
-
地球的直径多大 地球的尺寸大小是多少(12756千米)
-
猫屎咖啡收集自哪种猫?猫屎咖啡多少钱一杯
-
三星Note20系列再曝一亿像素保留但100倍变焦没戏了
-
中国移动x成都远洋太古里5G网络体验活动
-
脚踩花椒的好处和坏处 脚踩花椒的注意事项有哪些
-
处女座为什么被黑?几大主要原因告诉你答案
-
太屑了是什么梗:比人渣还要渣是屑(对反派的愤慨)
-
已被破解的未解之谜:神秘的麦田怪圈其实是这样出现的
-
月亮加星星是什么天气?天气预报有月亮有星星代表什么
-
黄河的源头在哪里 源自青海省青藏高原的巴颜喀拉山脉
-
海王星附近的巨型飞船 沙漏形物体不断翻滚旋转(外星飞船)
-
8张至今无法解释的神秘照片,时间旅行的证据,月球上的幽灵照片
-
人工降雨的原理是什么?
-
水晶跑车真的存在吗?水晶打造内里清晰可见
-
戒烟7天后身体的变化 戒烟好处有哪些(改善肺功能)
-
涡状星系位于何处?距离地球2300万光年远(猎户座内)
-
吃莲子心的禁忌有哪些 服用莲子心的注意事项
-
新发现的纳斯卡线已经隐藏沙漠数千年了,它们是远古文明的证据?
-
牛肉包子用什么部位的牛肉 牛肩肉牛胸肉或里脊肉
-
孙悟空最初那么厉害 为什么后来变弱了很多
-
太阳在膨胀还是在缩小?太阳大小是怎样变化的
-
【前沿物理】21世纪的物理学,迷失方向了吗?
-
秘鲁食人鱼吃小孩事件揭秘 真的有食人鱼将小孩吃掉?
-
佛跳墙怎么有酸味?佛跳墙有酸味怎么办(变质了)